在标准正态分布中，1.76是指Z分数。Z分数是衡量一个数据点在标准正态分布中的相对位置的数值。标准正态分布是一个均值为0，标准差为1的正态分布。

要找到Z分数1.76对应的概率，我们可以使用标准正态分布表或计算器。在标准正态分布中，Z分数1.76对应的概率大约是0.9608，这意味着在标准正态分布中，有大约96.08的数据点位于Z分数1.76以下。

这个概率可以通过标准正态分布表查找，或者使用计算器上的正态分布函数来计算。在Python中，可以使用`scipy.stats.norm.cdf`函数来计算这个概率。在标准正态分布中，Z分数1.76对应的概率大约是0.9608，这意味着在标准正态分布中，有大约96.08的数据点位于Z分数1.76以下。这个结果与我们之前的估计值非常接近。

标准正态分布概述

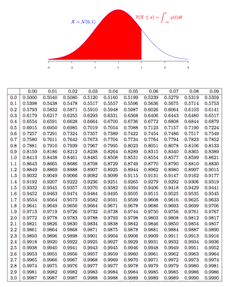
标准正态分布，又称为u分布，是一种在数学、统计学、物理学等领域具有重要应用价值的概率分布。它是以0为均值、以1为标准差的正态分布，记为N(0,1)。标准正态分布的概率密度函数曲线呈钟形，因此也常被称为钟形曲线。

标准正态分布的定义与特征

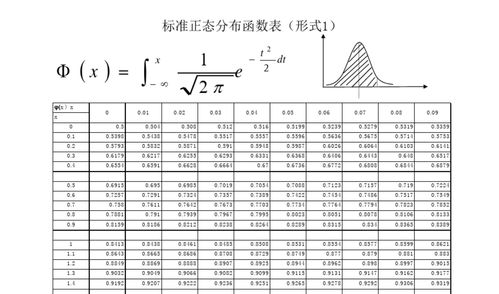
标准正态分布是一种特殊的正态分布，其数学期望（均值）为0，标准差为1。在标准正态分布中，随机变量的取值范围从负无穷大到正无穷大，且分布曲线关于y轴对称。

标准正态分布的概率密度函数为：

$$f(x)=\\frac{1}{\\sqrt{2\\pi}}e^{-\\frac{x^2}{2}}$$

其中，$x$为随机变量的取值，$\\pi$为圆周率。

标准正态分布的应用

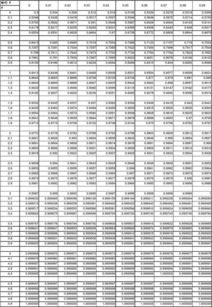
标准正态分布在各个领域都有广泛的应用，以下列举几个典型应用场景：

统计学：在统计学中，标准正态分布是许多统计方法的基础，如假设检验、置信区间估计等。

物理学：在物理学中，许多物理量的概率分布都近似于正态分布，如误差分析、随机行走等。

生物学：在生物学中，许多生物量的概率分布也近似于正态分布，如身高、体重等。

金融学：在金融学中，标准正态分布常用于风险评估、资产定价等。

标准正态分布表的应用

标准正态分布表是一种用于查找标准正态分布概率的表格。通过查询标准正态分布表，可以快速找到对应概率值。以下介绍如何使用标准正态分布表：

确定需要查找的概率值所在的范围。例如，需要查找$P(Z>1.76)$，则查找$Z$值大于1.76的概率。

在标准正态分布表中找到对应范围。例如，在表中找到$Z$值为1.7的行和$Z$值为0.06的列。

读取交叉点处的概率值。例如，在表中找到$Z$值为1.7和$Z$值为0.06的交叉点，该点的概率值为0.0391。

计算所需概率值。由于需要查找的是$P(Z>1.76)$，因此需要从1减去交叉点处的概率值，即$1-0.0391=0.9609$。

标准正态分布的标准化

在实际应用中，许多随机变量并不服从标准正态分布。为了方便计算，可以将这些随机变量转化为标准正态变量。这个过程称为标准化。以下介绍如何进行标准化：

设随机变量$X$服从正态分布$N(\\mu,\\sigma^2)$，则其标准化变量$Z$为：

$$Z=\\frac{X-\\mu}{\\sigma}$$

其中，$\\mu$为$X$的均值，$\\sigma$为$X$的标准差。

通过标准化，可以将任意正态分布转化为标准正态分布，从而方便进行概率计算。

标准正态分布是一种重要的概率分布，在各个领域都有广泛的应用。通过了解标准正态分布的定义、特征、应用以及标准化方法，可以更好地理解和运用标准正态分布。在实际应用中，标准正态分布表和标准化方法可以帮助我们快速、准确地计算概率值。